一种基于有限元软件屈曲分析求解铝合金受弯构件整体稳定系数的方法--技术文章--豪典设计室

摘要：鉴于《铝合金结构设计规范》GB 50429-2007（以下简称规范）对受弯构件的整体稳定系数的计算比较复杂，且规范公式仅适用于对称截面以及单轴对称截面绕对称轴弯曲的情况，对不对称异形截面在实际工程设计中不具有可操作性，本文提出一种利用有限元软件对异形截面建立三维有限元实体模型，采用SAP2000程序对模型进行屈曲分析，从而求得构件的弯扭稳定临界弯矩Mcr，再利用规范附录C中公式C-1、C-2、C-3来求得受弯构件的整体稳定系数φb。
关键词：铝合金梁；整体稳定；有限元法；屈曲分析；不对称截面

　　本文作者：王治明赵华
　　不对称异形截面铝合金梁整体稳定系数计算是一个比较复杂的过程，通常不借助计算机辅助程序很难完成，本文主要目的是探索目前在工程实际设计过程中如何快速、有效地确定铝合金简支梁的弯扭稳定临界弯矩，从而确定铝合金简支梁的整体稳定系数φb，首先我们先确定该方法的可行性，方法是采用H型截面分别按规范公式[1]和建立有限元三维模型进行弯扭稳定临界弯矩计算[4]，对结果数值进行对比分析，从而判断该方法的可靠性。而后利用已求得的简支梁的弯扭稳定临界弯矩Mcr，结合规范附录C中公式C-1、C-2、C-3来求得受弯构件的整体稳定系数φb，用于工程结构计算中的受弯构件整体稳定验算中，公式

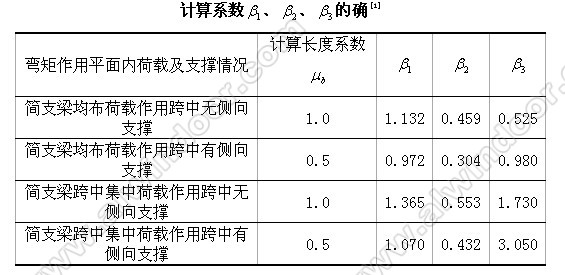
　　2 简支梁的弯扭稳定临界弯矩计算采用有限元软件计算
　　2.1在计算程序中输入构件的材料参数，需要说明的是一般计算程序可以自动计算一些材料参数[4]，这时发现这些值可能与规范有些出入，这其中的原因是规范中的值为取整的近似值（完全满足结构设计精度要求），而软件则采用计算值，两则差别不大，可以采用局部调整参数，以拟合规范。
　　2.2建立有限元三维实体模型，并适当调整网格划分，以求得到较为精确地结果，一般来讲，网格划分得越精细，计算结果越逼近精确解，但网格划分太精细将带来分析数据量很大[4]，结合计算机性能的特点，确定合理的网格划分。
　　2.4模拟平面外支撑作用，采用约束平面外作用点的水平位移。
　　2.5建立Bucking分析工况。
　　2.6分析完成后提取弯扭屈曲因子，计算得到临界弯矩。
　　3 建立数据对比分析
　　3.1建立两种截面两种跨度不同荷载形式及不同平面外支撑条件的计算模型（共计8种分析模型），对比按照规范计算的结果与采用有限元软件计算得结果对比，分析以按规范计算得结果为基准数的误差百分比，具体分析数据见下表。

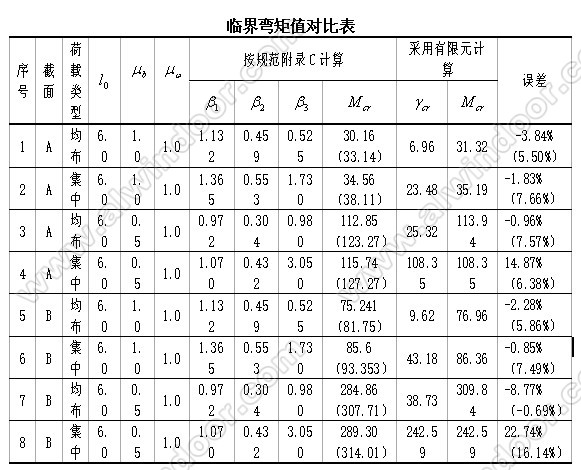
　　3.2通过分析可知，采用有限元软件计算的结果与按照规范计算结果比较接近，该结果具有一定的可靠性，可以用于实际工程分析中，同时4、5项结果偏差较大与建模时集中荷载作用位置与侧向支撑约束点位置有关，需要针对具体问题具体分析，综上所述，采用有限元软件求解构件的弯扭稳定临界弯矩是一种可行的办法，同规范计算公式得到的计算结果一样，采用有限元软件求得的弯扭稳定临界弯矩也没有考虑结构中的残余应力和构件本身的初始缺陷的影响[3]，该部分对构件整体稳定的不利影响将在后面的整体稳定系数的计算公式中予以考虑，本文不予讨论，后面仅利用规范中的公式求解梁的整体稳定系数φb.
　　4 计算异形不对称截面简支梁的整体稳定系数
　　通过上面分析结论，我们利用有限元分析软件求解构件的弯扭稳定临界弯矩，结合规范公式求解构件的整体稳定系数，以满足铝合金工程的设计需要！下面我们按照有限元方法求解一异形截面铝合金梁的临界弯矩及整体稳定系数。

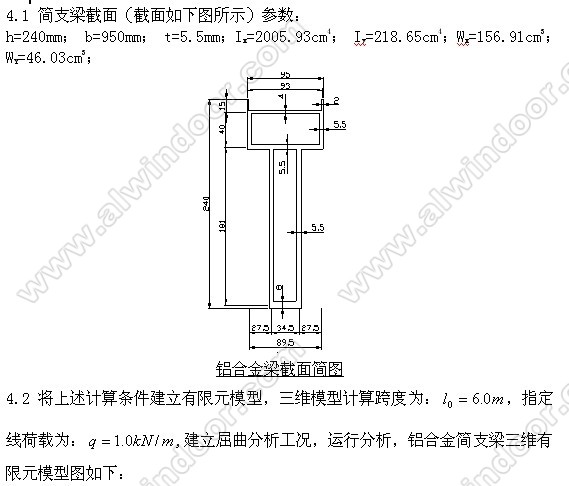
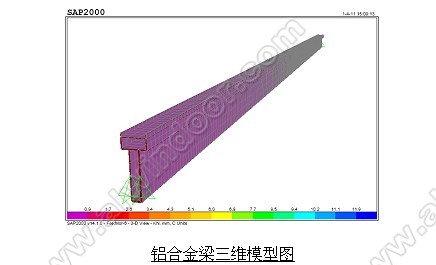
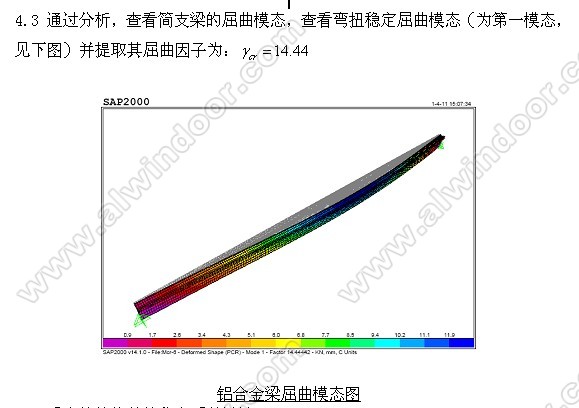
　　5 结语
　　通过计算结果数值分析，该方法计算受弯构件的整体稳定系数的方法是可行的，但鉴于缺少不对称异形截面的试验数据，需要工程师对异形不对称截面简支梁的整体稳定系数做更多的研究。算例中计算的异形不对称截面为闭口截面，故其整体稳定性较好！
　　参考文献
　　[1] GB 50429-2007 铝合金结构设计规范[S] .
　　[2] GB 50017-2003 钢结构设计规范[S] .
　　[3] 陈骥.钢结构稳定理论与设计[M] .3版.北京:科学出版社，2006
　　[4] 北京金土木软件技术有限公司.SAP2000中文版使用指南[M] .1版. 北京:人民交通出版社，2006